Appendix G

[Reprinted, with the generous permission of Cambridge University Press, from: Leonid Hurwicz and Stanley Reiter, 2006, Designing Economic Mechanisms, Cambridge University Press, unnumbered page immediately after the front cover, and pp. 1-7.]

Designing economic mechanisms

A mechanism is a mathematical structure that models institutions through which economic activity is guided and coordinated. There are many such institutions; markets are the most familiar ones. Lawmakers, administrators and officers of private companies create institutions in order to achieve desired goals. They seek to do so in ways that economize on the resources needed to operate the institutions, and that provide incentives that induce the required behavior. This book presents systematic procedures for designing mechanisms that achieve specified performance and economize on the resources required to operate the mechanism, i.e., informationally efficient mechanisms. Our systematic design procedures can be viewed as algorithms for designing informationally efficient mechanisms. Most of the book deals with these procedures of design. Beyond this, given a mechanism that implements a goal function in Nash equilibrium, our algorithm constructs a decentralized, informationally efficient mechanism that implements the goal function in correlated equilibrium.

======================================================

Introduction

This book presents an approach to the design of decentralized, informationally efficient economic mechanisms. We provide a systematic process by which a designer of mechanisms, who is presented with a class of possible situations by a client (perhaps a private agent, or a government) and with the client's aims and objectives, can produce informationally efficient decentralized mechanisms that achieve the client's aims in that class of situations.

HISTORY

Formal treatment of economic mechanisms and mechanism design began with Hurwicz's paper (1960). The background against which that paper was set included a debate on the comparative merits of alternative economic systems. The main participants in that debate included Lange (1938) and Lerner (1937, 1944) on one side, and von Mises (1920, 1935) and Hayek (1935, 1945) on the other. Hurwicz's paper provided for the first time a formal framework in which significant issues in that debate could be addressed. In a subsequent paper, Hurwicz (1972) treated the formal theory of mechanisms again. The problem is to select a mechanism from a set of alternative possible mechanisms. A mechanism is viewed as a value of a variable whose domain of variation is a set of possible mechanisms. Informational tasks entailed by the mechanism imply costs in real resources used to operate the mechanism (as distinct from the resources used in economic production and other real economic activities). Desiderata by which the performance of a mechanism is evaluated also come into play. Hurwicz recognized the fact, emphasized in the earlier debate, that information about the economic environment, the facts that enable or constrain economic possibilities, such as resource endowments and stocks of goods inherited from the past, and individuals' preferences for goods, is distributed among economic agents. It is obvious, but nevertheless worth saying, that those who do not directly observe some aspect of the prevailing environment do not have that information to guide their actions unless it is communicated to them by someone who does directly observe it.

Hurwicz introduced a formal model of a process of communication that incorporated this constraint – a dynamic message exchange process modeled after the Walrasian tatonnement. He used the term privacy (suggested by the inability of one to observe the private information of another) to refer to this restriction. His 1960 model includes as a formal element a language used for communication. The elements (words) used in that language are resource flow matrices which model production and exchange of commodities among the agents. He imposed restrictions on the language and on the functions used to model the communication process in order to generalize properties of the competitive mechanism that are deemed desirable.[1]

Hurwicz (1972) also recognized that dispersion of private information among economic agents can create incentive problems. He formalized this class of problems by introducing game forms as mechanisms, and also the concept and analysis of incentive compatibility of mechanisms.

Although the original formulation includes a tatonnement-like exchange of messages, attention soon focused on statics, that is, on the task of recognizing the equilibria of message exchange processes, rather than on the task of finding equilibria. In this literature, the verification scenario isolates the problem of recognizing equilibrium, or solution, from the process of finding equilibrium. In a verification scenario each agent reacts to an announced message by saying yes or no. The responses verify a proposed equilibrium when all agents say yes. (In the language of computer science a verification scenario is a nondeterministic algorithm.)

Mount and Reiter (1974) considered mechanisms that realize a given goal function. (Realize is the term used to refer to a situation in which the outcomes of the mechanism are precisely those specified by the goal function when agents do not attempt to use their private information strategically. The term implement is used when agents behave strategically.) Defining informational decentralization in terms of the structure of the language, and of related restrictions on permissible messages, as is done in Hurwicz (1960) creates two classes of mechanism: decentralized and not decentralized. Instead, Mount and Reiter provided a mathematical characterization of privacy-preserving message correspondences, and a concept of the informational size of a space. This formalization requires all mechanisms to be privacy preserving. It allows privacy-preserving mechanisms to be compared according to the informational sizes of their message spaces, and thereby creates an ordering of mechanisms by the informational size of their message spaces.[2]

The Mount-Reiter concept of the informational size of spaces (and other related concepts) applies to finite spaces, and to continua, including Euclidean spaces and more general topological spaces. They applied it in the 1974 paper to the competitive market mechanism in a class of pure exchange environments, a class in which the message space is Euclidean. Thus, an agent in a message exchange process could send signals based on his private information to another agent, at a cost that is increasing in the size of the messages. In some cases, that communication might require unfeasibly large messages. (This observation also applies to verification scenarios, with suitable adjustments.) This formulation produces an ordering of mechanisms, instead of classifying them as decentralized and not decentralized. Since then, the term informationally decentralized has come to be used for mechanisms whose communications respect privacy, and the size of the message space is used to indicate the real costs of communication. Mount and Reiter assumed, as in Hurwicz, that the initial distribution of information about the prevailing environment is given, and, as in Hurwicz, required that privacy be respected.

The mathematical characterization of privacy-preserving mechanisms (now called decentralized mechanisms) defines a structure of product sets in the space of environments (the parameter space). The relationship between product structures in the parameter space and privacy-preserving (henceforth decentralized) mechanisms is central to the design of mechanisms.

As already noted, the set of mechanisms from which a mechanism can be chosen is a formal element in the Hurwicz approach. One way to think of the problem is to construe the choice of economic organization as a problem of constrained optimization. In this view, there is a set of alternative mechanisms, each required to satisfy certain structural constraints (for instance ,privacy preservation), a set of environments, an objective function (the: goal function), and, for each candidate mechanism, the real costs (in resources) of operating that mechanism. The problem is to find one or more mechanisms in the set of available mechanisms whose outcomes in each environment match those specified by the goal function for that environment, and also minimize, in a vectorial sense, the real costs of operating the mechanism. But generally the set of mechanisms is not known. Some elements in this set might be known mechanisms, for instance, the competitive market mechanism, or one or another version of central planning mechanisms; but this short list surely does not exhaust the universe of conceivable mechanisms. Therefore we must seek a method or methods of discovering, or constructing, the elements of that set that are capable of realizing the given goal function.

This task requires that, among other things, we identify the determinants of the real costs of operating each mechanism. Resource costs have been identified as generated by:

• The need for agents to observe the part of the environment to which they have direct access. The precision with which agents must perform this observation determines part of the real cost of operating the mechanism.
• The amount of communication required by the mechanism. The informational size of the message space required has been taken as an indicator of this cost.
• The information processing, including computation, required for each agent to decide whether to say yes or no to an announced message. This dimension of cost is studied in Mount and Reiter (2002) and is not treated formally in this book, although it is commented on in places.
• The losses that arise because of deviation from full realization of the specified goals when agents behave strategically.
• Enforcement of rules of the game, when agents behave in ways that violate those rules.

A second formal element is the set of environments under consideration, and the goal function defined on that set of environments. More generally goals can be formalized by a correspondence. Analysis in which goals are represented by a correspondence usually reduces to analysis of selections (functions) from that correspondence. In this book we restrict attention to goal functions. Goals can arise in a wide variety of contexts. Some familiar ones arise in the context of neoclassical economic theory. Some arise in the context of organizations that are themselves part of a larger economic system, for example, firms, government agencies, nonprofit entities, and other institutions. Legislation can define socio-economic or political-economic goals. These considerations give emphasis to the need for systematic methods of discovering or designing new mechanisms, in a variety of formal (mathematical) settings.

Reiter realized in 1977 that the mathematical condition (given in Mount and Reiter 1974) that characterizes privacy-preserving message correspondences can be used to design decentralized mechanisms. He showed the relationship between a product structure, or an indexed production structure, and decentralized mechanisms in examples with two different goal functions. This discovery has led to an approach to systematic design of decentralized mechanisms, specifically, to the discovery of an algorithm (with variants) that accepts a finite set of agents, a factored environment space, and a goal function, and puts out one or more informationally decentralized mechanisms that realize the goal function. That is, the algorithm's output is a mechanism whose output in each environment recognizes the outcome specified by the goal function for that environment.

A decentralized mechanism that realizes a given goal function (it is implicit that the set of agents and the factorization of the space of environment are given) is itself an algorithm. It can be visualized as a machine that accepts as input an environment, and a possible value of the goal function at that environment, and produces as its output either yes or no. Yes, if the candidate value of the goal function is the one prescribed by the goal function, and no otherwise. This machine is presented graphically in Figure 1.

Figure 1. Machine 1: Nondeterministic algorithm.

An algorithm for designing such mechanisms can also be represented graphically as a machine that accepts as input a set of agents, a (factored) set of environments, and a goal function and produces as output a machine of the kind shown in Figure 1 – a decentralized mechanism that realizes the given goal function. This second machine is shown in Figure 2.

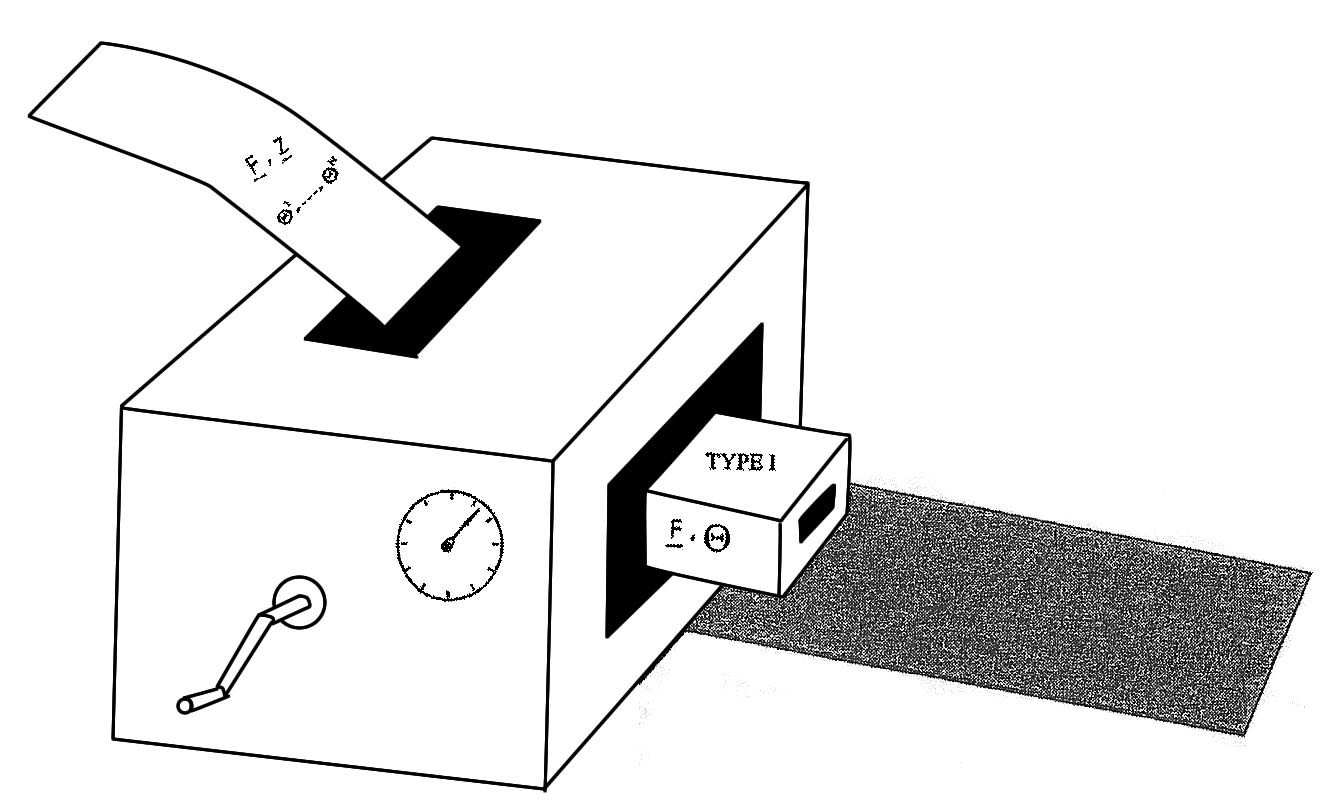
Figure 2.[3] Machine II: Algorithm for producing type I Mechanisms

Reiter presented these ideas to Don Saari, who then suggested using methods of calculus on manifolds, including methods from differential geometry, and the theory of foliations, specifically the Frobenius theorem on integrable distributions (see Warner 1971), to develop an approach to mechanism theory based on parameter-indexed product structures. Reiter also discussed these ideas with K. Mount, who helped him clarify certain mathematical elements.The research program opened by these ideas led first to joint works by Hurwicz, Reiter and Saari (1980). Steven Williams, at that time a student of Saari, provided a proof of a conjectured extension of the Frobenius theorem to products of distributions and the corresponding product interoperable distributions. Subsequently, Saari (1984) published a paper using a somewhat different mathematical apparatus. These approaches to mechanism design in one way or another entail solving systems of partial differential equations. Steven Williams followed the calculus on manifolds approach. His work is presented in a forthcoming book (Communication in Mechanism Design: a Differential Approach. Cambridge University Press) that extends and applies that approach.

We (Hurwicz and Reiter) undertook to develop a systematic method of designing decentralized mechanisms that do not rely on the heavy machinery of calculus on manifolds, or the theory of foliations, and that do not require solving partial differential equations. The results of that program are reported in this book. This book presents two basic algorithms called rectangles method and condensation method, respectively. This book presents several versions of the rectangles method algorithm in different mathematical settings. The methods presented here use more elementary mathematics to construct indexed product structures and from them construct informationally efficient decentralized mechanisms. Here informational efficiency includes observational efficiency and communication efficiency, with limited attention to a form of computational complexity called equation efficiency when environmental parameters are real numbers, and relations are given by equations.

Getting beyond this, we consider mechanisms that are incentive compatible, specifically mechanisms that implement a given goal function in dominant strategies, and also mechanisms that implement a goal function in Nash equilibrium. We apply our algorithms to modify a given mechanism that implements a given goal function (in dominant strategies or in Nash equilibrium) so that the modified mechanism is both informationally efficient and implements that goal function.

We present, for the case of finite environment spaces, an algorithm that modifies Nash-implementing mechanisms to make them informationally efficient, while preserving their incentive properties. It seems clear that the methods used in the finite case generalize to the case of Euclidean environment spaces; we present an example, but we have not carried out a general analysis.

[1] Marschak and Radner (1971) and Radner (1972a, 1972b, 1972c) took a different approach to mechanism design, called theory of teams. This approach incorporates uncertainty about environments, and about an agent's knowledge about the knowledge of other agents.

[2] For finite spaces, Euclidean spaces and topological spaces that have dimension this ordering is complete.

[3] Machine II is shown with a dial indicating that there are several settings of the machine. It is shown in Chapters 2 and 3 that the order in which we carry out certain steps of the algorithm for designing mechanisms can result in different machines of Type I.